用ODEs建模细胞周期（Julia代码）

卢旺收录于类别分子细胞生物学

2023-06-14 2023-06-14 约 538 字预计阅读 2 分钟

最近PubMed推送的一篇文章，正正好是我大二刚进实验室想要做的东西，当时苦于自身能力和知识的不足，就没有实践出结果。但着却一直是我在思考的问题，应该也会是我的终极目标之一——对细胞周期的调控过程进行动力学建模。

Williams, K. S., Secomb, T. W. & El-Kareh, A. W. An autonomous mathematical model for the mammalian cell cycle. J. Theor. Biol. 569, 111533 (2023).

读到文章后，第一时间就写代码重复了这篇文章的模型，好在原文对参数的描述很清晰，让我能够快速拿到和文章相似的结果

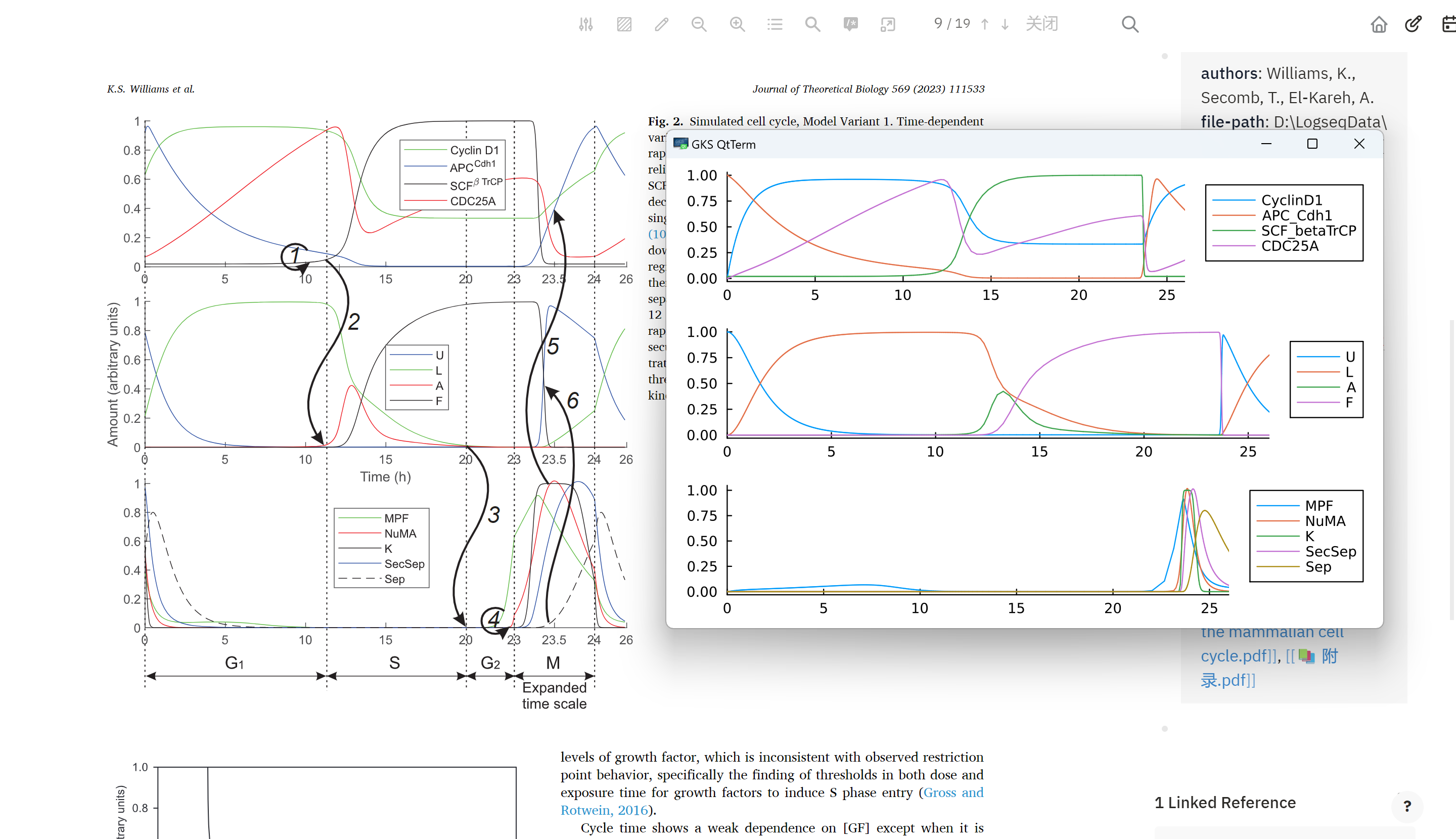
这里先贴出代码，之后有时间了再对着细胞周期调控机制，仔细梳理一下文章的思路

using SciMLBase
using OrdinaryDiffEq
using Plots

GF = 1.
k = [1. 2. 1. 0.02 1.5 5. 0.18 0.025 1. 50. 1. 2. 10. 20. 10. 1. 100. 1. 1.5 2. 2. 0.1 1. 1. 10. 2. 1. 50. 50. 2. 2. 1.]
n = [5. 5. 5. 5. 5. 5. 5. 5.]
C = [0.25 0.1 0.25 1. 0.1 0.1 0.001 1. 0.5 0.5 2.]

function cell_cycle!(dx, x, p, t)

    # x1 : CyclinD1
    # x2 : APC_Cdh1
    # x3 : SCF_betaTrCP
    # x4 : CDC25A
    # x5 : U
    # x6 : L
    # x7 : A
    # x8 : F
    # x9 : MPF
    # x10: NuMa
    # x11: K
    # x12: SecSep
    # x13: Sep

    dx[1] = k[1]*GF^n[1]/(C[1]^n[1]+GF^n[1]) - (k[2]*x[3]+k[3])*x[1]
    dx[2] = k[4] + k[5]*x[11] - (k[6]*x[3]+k[7]*x[1]+k[8])*x[2]
    dx[3] = k[9] - (k[10]*x[2]^n[2]/(C[2]^n[2]+x[2]^n[2]) + k[11])*x[3]
    dx[4] = k[12]*x[1] - (k[13]*x[2]+k[14]*x[3]*x[7]+k[15]*x[5]+k[16])*x[4]

    # v1
    RFU = k[17]*x[8]*x[2]^n[3]/(C[3]^n[3]+x[2]^n[3])
    RUL = (k[18]*x[5]*x[1]/(1+x[7]/C[4]))*(x[2]/(C[5]+x[2]))
    RLA = (k[19]* x[6] *x[4]/(1+x[7]/C[4]))*(x[3]^n[4]/(C[6]^n[4]+x[3]^n[4]))
    RAF = k[20]*x[3]*x[7]

    dx[5] = RFU - RUL
    dx[6] = RUL - RLA
    dx[7] = RLA - RAF
    dx[8] = RAF - RFU

    # v2
    # RAU = k[20]*x[3]*x[7]
    # RUL0 = k[17]*x[5]*x[10]
    # dx[5] = RAU - RUL0

    # RL0L = (k[18]*x[6]*x[1]/(1+x[7]/C[4]))*(x[2]/(C[5]+x[2]))
    # dx[6] = RUL0 - RL0L

    dx[9] = (k[21]*x[3]+k[22]*x[4])/(1+(x[7]/C[7])^n[5]) - (k[23]*x[2]+k[24])*x[9]
    dx[10] = k[25]*x[9]^n[6]/(C[8]^n[6]+x[9]^n[6]) - (k[26]*x[2]+k[27])*x[10]
    dx[11] = k[28]*x[10]^n[7]/(C[9]^n[7]+x[10]^n[7])*(1-x[11]) - (k[29]*x[13]^n[8]/(C[10]^n[8]+x[13]^n[8]))*x[11]
    dx[12] = (k[30]*x[10]^n[7]/(C[9]^n[7]+x[10]^n[7]))*(C[11]-x[12]) - k[31]*x[2]*x[12]
    dx[13] = k[31]*x[2]*x[12] - k[32]*x[13]

end

x_0 = [0.; 1.; 0.; 0.; 1.; 0.; 0.; 0.; 0.; 0.; 0.; 0.; 0.]
# x_0=[0.6; 0.8; 0.01; 0.1; 0.8; 0.2; 0.; 0.; 0.5; 0.5; 0.4; 1.; 0.6]
tspan = (0.0, 200.0)
prob = ODEProblem(cell_cycle!, x_0, tspan)
sol = solve(prob, Tsit5())
# plot(sol)

solmat = reduce(hcat,sol.u)'

p1 = plot(sol.t, solmat[:,1:4], label=["CyclinD1" "APC_Cdh1" "SCF_betaTrCP" "CDC25A"])
p2 = plot(sol.t, solmat[:,5:8], label=["U" "L" "A" "F"])
p3 = plot(sol.t, solmat[:,9:end], label=["MPF" "NuMA" "K" "SecSep" "Sep"])
plot(p1, p2, p3, layout=(3,1), background_color = :transparent)
plot!(legend=:outerright, grid=false)
xlims!(0,26)
# xlabel!("Time(Hour)")