MDF | 01. 概率是热力学的基础

对统计热力学的基本认识
-
很多现象,例如物质相变、油水分离、晶体生长、化学反应(酶促反应)、弹簧收缩或反弹等等,这些过程之所以可以发生,其本质上是存在着推动该过程发生的“力”,而认识、测量、计算这种“力”的方法就是统计热力学
-
之所以统计热力学是很复杂的学科,是因为对这些过程发生趋势和平衡的描述不能只用到那些只管可测量的性质(比如密度、温度、压力、分子半径、平衡常数等),还需要用到一些更为抽象的、不能直接测量的性质(能力、熵、焓、自由能)
-
熵是统计热力学中最为基础的一个概念,它描述了物质趋于混乱的程度
概率(高中数学)
- 概率的定义需要一个事件主体以及事件可能的所有结果,在对结果进行分类后,便可以定义出特定结果出现的概率:
$$ p_A = \frac{n_A}{N} $$
-
概率值是一个0-1之间的数字,0表示事件结果不可能出现,1表示一定会出现
-
事件之间的关系:
-
互斥关系(exclusive),A发生时B一定不发生,B发生时A一定不发生
-
全概率(collectively exhaustive),即结果A1,A2,……,At组成了所有的可能,不会有其他结果出现时,他们就是全概率的
-
独立(independent),事件结果A和另一事件结果B之间不存在任何相互影响的关系
-
多样性(重数,multiplicity),事物的结果是具有多个性质的,不同方面可能有几种可能,那么将这些方面综合来看就有着相乘的关系。比如说有两种不同形状、三种不同颜色的小汽车,那么最终一共就有2×3=6种小汽车
-
-
基本事件的概率的计算(Elementary Event)
- 加法原则:如果事件结果互斥,则多个事件的概率之间可以相加
$$ p(A\ or\ B\ or\ …\ or\ E) = \frac{n_A+n_B+…+n_E}{N} =p_A+p_B+…+p_E $$
- 乘法原则:两件事同时发生的概率用乘法(并没有要求两事件之间相互独立)
$$ p(A\ and\ B\ and\ …\ and\ E)=(\frac{n_A}{N})(\frac{n_B}{N})…(\frac{n_C}{N})=p_A \cdot p_B \cdot … \cdot p_E $$
-
复合事件的概率计算(Composite Event)
-
复合事件是对基本事件分类后,得到的具有相对复杂的关系的多个结果,通常不能直接用加法或乘法计算,比如下面这个例子
例1.7:两次骰子结果出现1或4Q: 计算投两次骰子,结果中出现第一次为1或第二次为4的概率?
A1(直接计数): 两次投掷结果是相互独立的,因而将两次投掷认定为一个基本事件时,一共有36种结果。在这36种结果中,出现第一次为1或第二次为4的情况有11种,因而这个问题的答案是$\frac{11}{36}$
A2(拆解事件): 思考时也可以该符合事件拆分成可以用乘法加法运算几部分:
事件A:第一次结果为1 AND 第二次结果不为4 $$ p_A = (\frac16)(\frac56) $$ 事件B: 第一次结果不为1 AND 第二次结果为4 $$ p_A = (\frac56)(\frac16) $$ 事件C:第一次结果为1 AND 第二次结果为4 $$ p_A = (\frac16)(\frac16) $$
三部分互斥,组成了问题事件的结果,因而只需再将三部分加起来即可
A3(找反面事件): 也可以直接思考这个问题的反面,即“第一次不是1 AND 第二次不是4”,随后用1减去该概率
-
条件概率(大学概率论基础)
-
当一件事A的发生依赖于另一事件B,则对事件A的描述可以是对其的直接观察$p(AB)$,也可以是在B一定发生时再观察A的概率$p(A|B)$
-
前者被成为联合概率(Joint probability),指代事件A和B同时发生的概率,$p(AB)$是对$p(A\ and\ B)$的简写
-
后者被称为条件概率,其中“B一定发生”是条件
-
对这两个事件A和B使用乘法法则,可以得出联合概率和条件概率的计算关系,这一关系被称为贝叶斯法则。其原理是依据事件A发生时,事件B一定发生,即是有关系$ p(A|B)=p(A) $
$$ p(AB) = p(A\cap B) = p(A|B)\cdot p(B) = p(B|A)\cdot p(A) $$
-
在上式表述的关系中,$p(B)$被称为先验概率 (priori probability),条件概率$p(A|B)$被称为后验概率 (posteriori probability)
-
另外,还有一个加法原则的基本关系式
$$ p(A\cup B) = p(A)+p(B)-p(A\cap B) $$
-
当事件A和B互斥,$p(A\cap B) = 0$,此时该式子就变为了上面说的加法原则的关系式
-
定义如下式子为相关度,用以描述B影响A的程度 $$ g=\frac{p(A|B)}{P(A)} = \frac{p(AB)}{p(A)P(B)} $$
- 当$g=1$时,说明B不影响A
- 当$g=0$时,说明B发生时,A一定不发生
- 当$0 \lt g \lt 1$,说明B的发生使A发生概率降低了,是负影响
- 当$g \gt 1$,说明B使A概率增高,是正影响
-
联合概率相加也可以用于求解特定事件发生的概率,其中$\bar A$表示事件A不发生,公式也可以用贝叶斯关系式展开
$$ p(B) = p(BA) + p(B\bar A) = p(B|A)p(A) + p(B|\bar A)p(\bar A)$$
例1.11:贝叶斯方法预测蛋白性质(Just a toy example)Q: 假设你发现了一种特殊的蛋白结构叫做
heli-coil h,这种结构很稀有,你在5000个蛋白结构中才找到20个类似的结构,即$p(h)=0.004$。同时,在找到的20个序列中,你发现有19个结构都带有一种氨基酸序列特征(motif)叫做sf,即$ p(sf|h)=0.95$。现在你认为这个序列特征sf是导致heli-coil h出现的关键因素,你应该如何证明你的观点?A: 在这个问题中,需要计算的关键数字应该是在序列
sf出现时h也同时出现的概率,即$p(h|sf)$。根据贝叶斯公式,$$ p(h|sf) = \frac{p(sf|h)p(h)}{p(sf)} = \frac{p(sf|h)p(h)}{p(sf|h)p(h)+p(sf|\bar h)p(\bar h)} $$
还需要知道$p(sf|\bar h)$的概率,即不存在这个
heli-coil h结构的蛋白中,有多少蛋白是含有sf序列特征的,假设这个数字是$p(sf|\bar h)=0.001$,可以得到$$ p(h|sf) = \frac{(0.95)(0.004)}{(0.95)(0.004)+(0.001)(0.996)}=0.79 $$
于是可以得出结论,在含有
sf序列特征的所有蛋白中,有约80%都可以形成heli-coil h结构
排列组合(高中数学)
-
排列组合是一种快速计算事件总结果数的一种方法,其包含有两个问题:排列问题和组合问题
-
阶乘$N! = 1\cdot 2\cdot 3 \cdot … \cdot N$,定义$0!=1$
-
排列数:从m个物品中选择n个进行排序,可以得到的$A_m^n$种结果
$$ A_m^n = \frac{m!}{(m-n)!} = m\cdot (m-1) \cdot (m-2) \cdot … \cdot (m-n+1)$$
- 组合数:从m个物品中选择n个时,可以得到$C_m^n$种结果
$$ C_m^n = \frac{A_m^n}{A_n^n} = \frac{m!}{n!(m-n)!} = \frac{m\cdot (m-1) \cdot (m-2) \cdot … \cdot (m-n+1)}{n\cdot (n-1) \cdot (n-2) \cdot … \cdot 1}$$
-
Q: 单词$cheese$是有6个字母组成的,如果将6个字母随机打乱重新排序,有多少种排序方法仍旧可以得到正确拼写?
A: 一共有$A_6^6=720$种可能,但其中有3个字母e是不需要排序的,因而需要再除以$A_3^3=6$,一共120种可能可以得到正确拼写
Q: 将n个没有区别的小球放进M个盒子中,有多少种方法?
Ref: Bosons是一种特殊的粒子(玻色子),爱因斯坦模型是说有n个玻色子可能归属于M个能级(可以有多个相同的粒子处于同一能级)
A: 高中时很经典的问题,可以用插板法 来解决,即可以把装入M个盒子看成是在n个元素的序列上插入(M-1)块板,将其分隔成M块,于是问题就转变为了n个球连同(M-1)块板的排序问题,综合利用排列组合,答案为 $$ W(n,M) = \frac{A_{n+M-1}^{n+M-1}}{A_n^n\cdot A_{M-1}^{M-1}} = \frac{(n+M-1)!}{n!\cdot (M-1)!}$$
概率分布函数(大学概率论内容)
-
在特定的事件中,可以在明确一些变量作为随机变量,其可以是具有特定物理含义的量,也可以仅仅只是一个编号标识。在选定随机变量后,可以找到概率值和随机变量之间的关系,这一关系被称作概率分布函数 ,其包含了该概率问题的全部信息
-
根据随机变量的类型,可以分为离散型概率分布和连续型连续型
-
在连续型分布函数中,p(x)被称为概率密度,其并不对应真正的概率值,只有在对随机变量进行积分后,才可以被称为概率,即当随机变量取值为$x+dx$的概率,使用如下公式计算随机变量$x$取值在范围$[a,b]$的概率:
$$p(a\le x \le b) = \int_a^b p(x)dx $$
-
有时候分布函数在全x范围积分后并不等于0,需要再进行一步标准化(归一化,normalized)
-
有一些概率分布在自然界中高频出现,这里主要先提两个,因为这是“熵”概念引出的基础
- 二项分布:每一次实验相互独立,且仅具有两个互斥的结果,这种事件被称为伯努利事件。假设有两互斥的结果成功和失败,其中成功的概率为$p$,失败则为$1-p$,现实验N次,有n次成功的概率符合二项分布,其公式为
$$ p(n,N) = C_N^n \cdot p^n\cdot (1-p)^{N-n} = \frac{N!}{n!(N-n)!}\cdot p^n \cdot (1-p)^{N-n} $$
-
其中$\frac{N!}{n!(N-n)!}$是二项式系数,该公式可以理解为将$p$和$1-p$带入二项式定理得到的;根据N的不同上下排列,绘制出的图形为杨辉三角
-
多项式分布:当事件有$t$种互斥的结果,N次实验中,每种结果出现的次数为$n_1$,$n_2$,……,$n_t$(全部相加即为$N$)的概率为:
$$ p(n_1, n_2, …, n_t, N)=(\frac{N!}{n_1!n_2!…n_t!})p_1^{n_1}\cdot p_2^{n_2}\cdot … \cdot p_t^{n_t} $$
-
概率分布函数$p(x)$的$n$阶矩为
$$ <x^n> = \int_a^b x^n p(x)dx = \frac{\int_a^b x^n g(x) dx}{\int_a^b g(x)dx} $$
计算$n$阶矩时,可以使用标准化后的概率分布函数$p(x)$带入左边式子计算;但当分布函$g(x)$数并未标准化时,也可以使用右边的式子
-
当$n=0$时,$<x^0>=\int_a^b p(x) dx=1$,即任何概率分布函数的零阶矩等于0
-
当$n=1$时,$<x^1>=\int_a^b x\cdot p(x) dx$,该数值被称为随机变量的均值、期望、一阶矩
-
对于矩的计算,不仅仅可以针对随机变量$x$进行计算,也可以针对以$x$针对自变量为$x$的函数$f(x)$进行计算,例如:
$$ <f(x)>=\int_a^b f(x)p(x)dx = \frac{\int_a^b f(x)g(x)dx}{\int_a^b g(x)dx} $$
- 还有两个很有用的、关于计算均值的式子
$$ <af(x)>=\int af(x)p(x)dx = a\int f(x)p(x)dx = a<f(x)> $$ $$ <f(x)+g(x)> = \int [f(x)+g(x)] p(x)dx = \int f(x)p(x)dx + \int g(x)p(x)dx = <f(x)>+<g(x)> $$
- 方差被定义为距离均值的离散程度,其中$a=<x>$,即$a$是均值(一阶矩),是一个常数;根据下面式子的推导,方差也等于二阶矩减去一阶矩的平方
$$ \sigma^2 = <(x-a)^2> = <x^2-2ax+a^2> = <x^2> -2a<x> + a^2 = <x^2> - <x>^2 $$
-
对方差开平方得到的值被称作标准差
-
更高阶的矩描述概率分布函数的不对称性
Q: 对于在$0\le x \le \infty $上的分布函数$g(x)=e^{-ax}$($a \gt 0$),求解均值
A: 首先标准化该函数,然后再计算一阶矩
$$ g_0=\int_0^\infty e^{-ax}dx = \left. -(\frac1a)e^{-ax} \right \vert _0^\infty = \frac1a $$
$$ <x>=\frac{\int_a^b x^ne^{-ax}dx}{1/a} = a \int_a^b x^n e^{-ax} dx = \left.-[e^{-ax}(x+\frac1a)]\right \vert_0^\infty = \frac1a $$
Q: 假设你有一个空间三维矢量,它可以在所有可能的角度$\theta$上自由地均匀定向,计算该矢量在特定轴(比如z轴)向上投影的平均长度
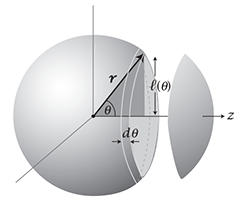
A: 对投影的描述可以用类似$\cos \theta$,$\cos^2 \theta$的量来描述。因为角度指向是均匀的,所以其指向的各个角度是与球面成比例的。围绕z轴的这个条带面积为$(rd\theta)(2\pi l)$,而$l=r\sin\theta$,因而该面积为$S=2\pi r^2 \sin\theta d\theta$。在0-90°时,当角度$\theta$变小一点儿时,面积也会变小一点。这个条带的面积占整个球面的面积,即是在$\theta$角度的概率
$$ p(\theta)=\frac{2\pi r^2 \sin \theta d\theta}{\int_0^\pi 2\pi r^2 \sin\theta d\theta} = \frac{\sin\theta d\theta}{\int_0^\pi \sin\theta d\theta} $$
因而$<\cos \theta>$的均值是
$$ <\cos\theta>=\int_0^\pi \cos\theta p(\theta) d\theta = \frac{\int_0^\pi \cos\theta \sin\theta d\theta}{\int_0^\pi \sin\theta d\theta} = \frac{\int_0^\pi \cos\theta \cdot -d\cos\theta}{\int_0^\pi -d\cos\theta} = \frac{\int_1^{-1} xdx}{\int_1^{-1}dx} = \frac{\left. \frac12 x^2 \right \vert_1^{-1}}{x\vert_1^{-1}} = 0 $$
各个方向会相互抵消,所以$<\cos \theta>$表现为0,为了更好表述该性质,可以使用$<\cos^2\theta>$的均值(类似均方根速度)
$$<\cos^2\theta> = \int_0^\pi \cos^2\theta p(\theta) d\theta = \frac{\int_0^\pi \cos^2\theta \sin\theta d\theta}{\int_0^\pi \sin\theta d\theta} = \frac{\left. \frac13 x^3 \right \vert_1^{-1}}{x\vert_1^{-1}} = \frac 13$$
常见分布举例
| 分布 | 描述 | 公式 | 图像 |
|---|---|---|---|
| 伯努利分布 | 伯努利事件概率为$p$,1次实验成功的概率 | $$g(n)=p^n\cdot (1-p)^{1-n} \\ \\ n=0, 1$$ | 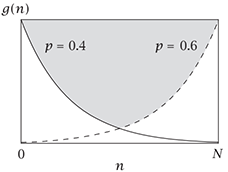 |
| 二项分布 | 伯努利事件概率为$p$,$N$次实验成功$n$次的概率 | $$ p(n)=C_N^n p^n \cdot (1-p)^{N-n} \\ \\ n=1,2,…,N $$ |  |
| 均匀分布 | 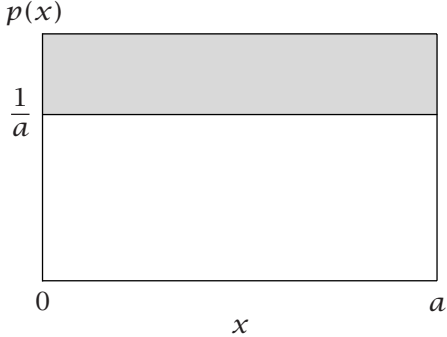 |
||
| 泊松分布 | 伯努利事件成功的概率是$a$,$n$次简单随机实验事件成功发生a次的概率,假设每次随机实验, | $$p(n)=\frac{a^n\cdot e^{-a}}{n!}$$ | 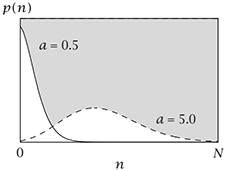 |
| 高斯分布 | ss | $$ p(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-x^2/2\sigma^2} $$ | 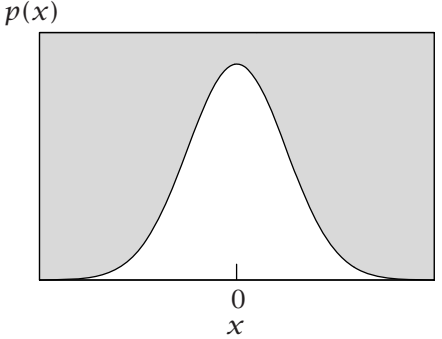 |
| 指数分布 玻尔兹曼分布 |
$$ p(x)=ae^{-ax} \\ x\ge 0 $$ | 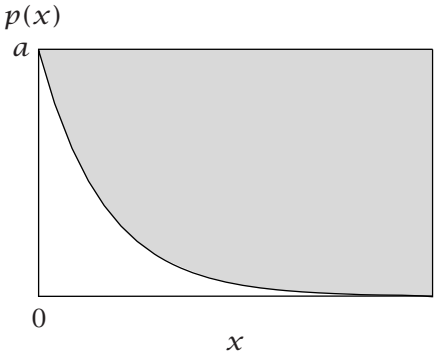 |
|
| 柯西分布 | 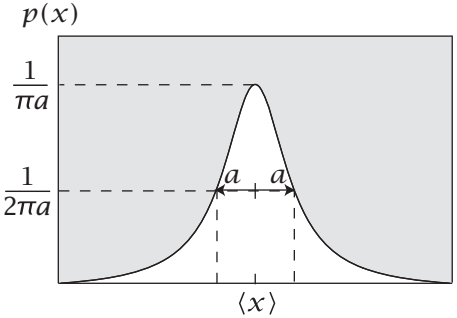 |
||
| 幂律分布 | 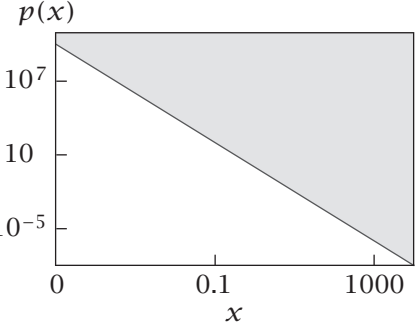 |
