MDF | 02. 极值原理与平衡状态

极值原理（Extremum Principles）

• 分子会通过构象变化、物理化学反应来改变两个关键的参数，一个是使得能量最低，另一个是熵最大。反过来，我们可以通过计算能量和熵，并且在数学上使函数达到极值，从而来预测分子的运动趋势，这一思路被称为极值原理

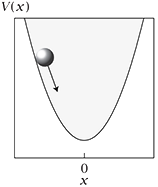
  例2.1：小球从高处滚落使能量降低

  对于质量为$m$，处于高度为$z$的小球而言，其重力势能$V(z)=mgz$，若其现在处于谷形结构中（该结构可以用$z=x^2$来描述），因而带入后有重力势能$V(z)=mgz=mgx^2$

  极值原理告诉我们，小球现在将会滚落到重力势能最小的位置。于是可以找到一个$x^*$使得重力势能$V(z)$最小。不难求解，当$x=0$使，能量最低

  

• 在上述案例中，水平位置$x$是问题分析过程中可以变化的量，称为自由度（degree of freedom）；与自由度概念相反的，即体系不能自由变化的量，或者说小球被控制或限制的因素，被称为限制量（constraint）

• 极值原理的数学含义，就是通过改变自由度，使特定函数在约束条件下，达到极值；体系可以拥有多个自由度或限制

平衡态（State of Equilibrium）

• 在上面的例子中，小球会从高处滚落到底部，并且处于底部位置，此时这个“底部的位置”就是该体系的一个平衡态，即体系趋向并保持的状态，此时净受力为0。

• 力是描述运动趋势大小的一个物理量，可以通过势能来定义（势能是力的积分，而力是势能的偏导数）

$$V(x) = -\int f(x) dx， f = -(\frac{\partial V}{\partial x})$$

• 有多种情况可以达到净受力为0，具体如下：

  • Stable：势能达到最小时的状态（但凡系统要离开这个状态，势能都必然增加），可以用如下式子寻找该状态（数学上用导数寻找最值的方法）

  $$ \frac{dV}{dx} = 0 \ and \ \frac{d^2V}{dx^2}=0 \ at \ x=x^* $$

  • Neutral：势能函数前后不再变化，为一个定值（flat），在改变状态时不影响势能状态

  $$ \frac{dV}{dx}=0 \ for\ all\ x $$

  • Metastable：势能达到极小值（全局上还存在更小的位置），其在小范围扰动下不会变化，但在大范围扰动后最终还是会倾向到势能最小值处

• 系统的稳定性不仅仅取决于受力是否为零，也取决于系统如何响应扰动（perturbation）（比如乒乓球很容易被微风吹走，但铅球就不会），上述不同的平衡态应对扰动的方式也不同

最大化多样性可以预测最可能发生的结果 –> 熵

在这一部分，会通过几个案例来说明极值原则。首先通过一个简单的掷硬币的案例，引出multiplicity的概念，并且简单引申出熵(entropy)，随后通过几个简单的例子来感受极值原则（具体指熵力）是如何影响系统运动的（包括气体扩散施压、分子混合扩散、橡皮的拉伸和回缩）

• （扔硬币的案例）现考虑投掷均匀的硬币4次，会得到4个结果，如HHHH或HTHH等，这些含有实验顺序的结果都是等概率的，其每种情况出现的概率为$ (1/2)^4 $。但若现在不考虑顺序，只考虑出现H或T的个数，哪一种组合（composition）出现的概率最大？如果投掷N次硬币呢？

  • 为了搞清楚哪种情况出现概率最大，需要计算每种情况出现的次数$W$（即为多样性，或翻译为重数，multiplicity）；记$n$为出现Head的次数，当$N=4$时：

    $n$	$W$	$\ln W$
    4	$\frac{4!}{0!4!}$	0
    3	$\frac{3!}{1!3!}$	1.386
    2	$\frac{2!}{2!2!}$	1.792
    1	$\frac{1!}{3!1!}$	1.386
    0	$\frac{0!}{4!0!}$	0

  • 当投掷$N$次硬币，出现$n$次Head一共有$W(n,N)$种情况，因而出现概率最大的情况是$W(n,N)$达到最大时（在$W(n,N)$达到最大时，$\ln W$也达到最大，因为自然对数是单调增函数）

    $$ W(n,N) = C_N^n = \frac{N!}{n!(N-n)!} $$

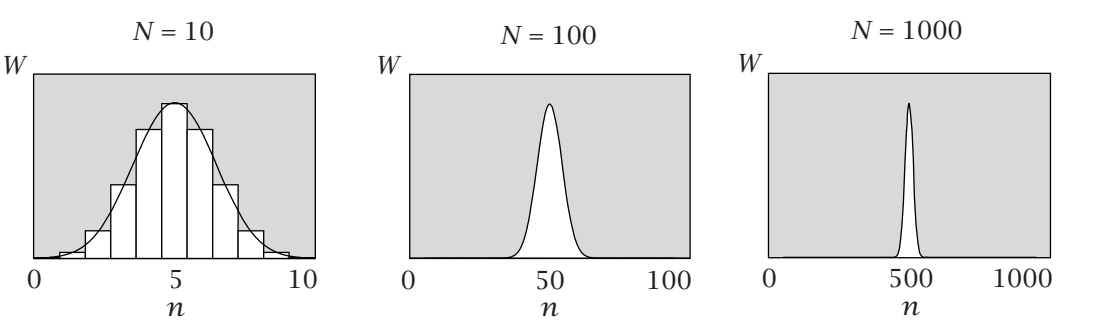
  • 根据计算，投掷结果最大概率出现的是一半Head一半Tail的情况，并且当投掷次数增多时，这个趋势越来越明显

    

  • 在该问题的分析中，我们发现只有当$n=\frac N2$时，函数$W(n,N)$才能取得最大值。其中$n$是该系统的自由度，其取值可以为$ 0 \le n \le N$

  • 值得思考的是，在每一次抛出硬币时，并不会感受到这种结果的趋势（或者说“力”的存在），但是在多次实验后，确实存在这样一种driving force来影响着结果的变化，这种影响趋势就是熵的本质

  • 即是说，寻找最大的$W$，在本质上和“能量最低原理”一样，也是在极值化一个趋势函数，进而寻找系统的稳态

• 借着上面案例，明确几个概念（专有名词）：

  • 微观状态（microstate）：指代某一次实验的具体结果，也就是上面说的“每种情况”，重数（Multiplicity）也因此被称为“微观状态数”。每一种微观状态都是等概率的。

  • 宏观状态（macrostate）：宏观状态是微观状态的集合，是可统计、可观测、可控制的，如只出现1次Head（$n=1$）的情况。

  • 在随后章节介绍的熵（Entropy）就是基于重数给出定义的，$S=constant \times \ln W$，熵的最大化就是对重数的最大化。

• 在接下来的几个例子中，为了简化问题，使用**晶格模型（lattice modle）**作为底层的思路，在该模型中：

  • 原子或分子被认为是硬质的小球
  • 空间被分割为了连续的格子（lattice sites），并且每个格子只能放下零个或一个小球
  • 两个格子之间相互独立
  例2.2：气体施压的案例 --> 气压

  Q：现有$N$个粒子占据了$M$体积的空间，如何考虑气压的形成？

  A：气体具有自发扩散的趋势，从而形成了气压。对气压的认识，可以从机械力的角度理解（气体分子对器壁的碰撞形成了气压），也可以在使用晶格模型简化问题后从最大多样性的角度理解（粒子为了最大化分布趋势）。现在假设有固定个数$N$的粒子，而容器的体积$M$不固定（即自由度），考虑如何最大化Multiplicity。该问题在本质上和抛硬币是一致的，对于连续的空间，每一个空间格子都会有两种状态，即被粒子占据或空着，其结果也是表现为一个状态的连续序列，如[vacant, occupied, occupied, …]

  因而，计算$N$个粒子占据了$M$体积的空间，可以有$W$种情况

  $$ W(N,M) = C_M^N = \frac{M!}{N!(M-N)!}$$

  假设现在有3个粒子，当$M=3$时，$W(3,3)=1$；当$M=4$时，$W(3,4)=4$；当$M=5$时，$W(3,5)=5$。发现当体积膨大时，重数也在对应的增大。即是说，如果当体系的体积具有一定选择时，膨大体积是顺应重数最大化趋势的一个策略。后面的章节会进一步深入该模型，去理解理想气体方程的原理。

  例2.3：分子一维扩散的案例 --> 化学势

  Q：假设现在有4个●和4个○充斥在有8个格子的空间中，在空间的正中间有一假想的透过屏障，统计在屏障两侧不同种小球的的可能情况？

  A：考虑3种情况：

  • 情况A：左右两边都是2黑2白

    $$ W_A = W(Left)\cdot W(Right) = C_4^2 C_4^2 = 36 $$

  • 情况B：左侧3黑1白，右侧3白1黑

    $$ W_B = W(Left)\cdot W(Right) = C_4^3 C_4^1 = 16 $$

  • 情况C：左侧全为黑球，右侧全为白球

    $$ W_C = W(Left)\cdot W(Right) = C_4^4 C_4^0 = 1 $$

  经过计算发现，最平均分配的情况A具有最高的重数，即是最有可能出现的情况；而情况C具有最强的不均匀分布则具有最小的出现概率。如果自由度是允许粒子在和格子间相互交换，那么重数就会趋于最大，不同粒子分布均匀。

  例2.4：橡皮弹性的案例

  Q：用最大化重数的原理，解释弹簧弹力的形成

  A：弹簧的伸缩问题可以看作是一个多聚体的折叠问题，可以想象将弹簧的一端固定在墙壁上，认为弹簧另一端所处的位置是自由度，有如下几种情况（configuration）

  

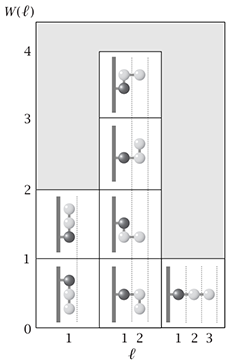
  发现，当长度为2时，其具有最多种状态。

练习题