分析化学 | 酸碱形体分布和pH关系

分布系数：平衡时溶液中某物种的平衡浓度占总浓度的分数 $$ \delta = \frac{[c_i]}{c_0}$$ 分布曲线：不同pH值溶液中酸碱存在形式的分布

import numpy as np
from matplotlib import pyplot as plt

一元酸解离分配

$$ HA \longrightarrow H^+ + A^- , K^\Theta_a=\frac{[H^+][A^-]}{[HA]}$$

对于$HA$,其分布系数为： $$\delta_{HA} =\frac{[HA]}{[HA]+[A^-]} =\frac{1}{1+\frac{[A^-]}{[HA]}} =\frac{1}{1+\frac{K^\Theta_a}{[H^+]}} =\frac{[H^+]}{[H^+]+K^\Theta_a}$$

对于$[A^-]$，其分布系数为： $$\delta_{A^-} =\frac{[A^-]}{[HA]+[A^-]} =\frac{1}{1+\frac{[HA]}{[A^-]}} =\frac{1}{1+\frac{[H^+]}{K^\Theta_a}} =\frac{K^\Theta_a}{[H^+]+K^\Theta_a}$$

# Ka = float(input('输入Ka：'))
Ka = 1.6e-5 # 默认数据为醋酸
pH = np.arange(0,14,0.1)
dHA, dA = [], []
for i in pH:
    H = 10**-i
    dHA.append(H/(H+Ka))
    dA.append(Ka/(H+Ka))

plt.figure(figsize=(8,5))
plt.plot(pH, dHA, label='HA'), plt.plot(pH, dA, label="$A^-$")
plt.xlim([0,14]), plt.ylim([0,1])
plt.xlabel('pH'), plt.ylabel('$\delta$'), plt.legend()
plt.show()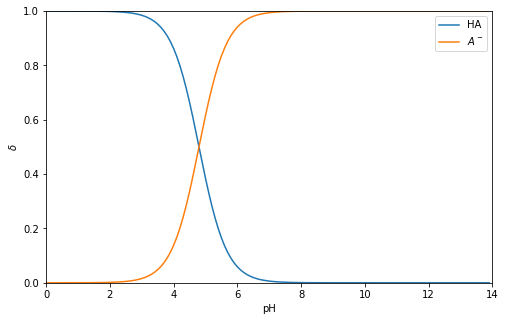

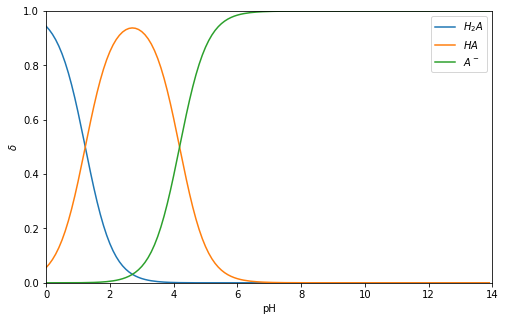
二元酸解离分配

$$ H_2A \longrightarrow H^+ + HA^- , K^\Theta_{a1}=\frac{[H^+][HA^-]}{[H_2A]}$$ $$ HA^- \longrightarrow H^+ + A^{2-} , K^\Theta_{a2}=\frac{[H^+][A^{2-}]}{[HA^-]}$$

对于$HA$,其分布系数为： $$ \delta_{H_2A} =\frac{[H_2A]}{[H_2A]+[HA^-]+[A^{2-}]} =\frac{1}{1+\frac{[HA^-]}{[H_2A]}+\frac{[A^{2-}]}{[H_2A]}} =\frac{1}{1+\frac{K^\Theta_{a1}}{[H^+]}+\frac{K^\Theta_{a1}K^\Theta_{a2}}{[H^+]^2}} =\frac{[H^+]^2}{[H^+]^2 + [H^+]K^\Theta_{a1} + K^\Theta_{a1}K^\Theta_{a2}} $$

对于$[A^-]$，其分布系数为： $$\delta_{HA^-} =\frac{[H^+]K^\Theta_{a1}}{[H^+]^2 + [H^+]K^\Theta_{a1} + K^\Theta_{a1}K^\Theta_{a2}}$$

对于$[A^{2-}]$，其分布系数为： $$\delta_{A^{2-}} =\frac{K^\Theta_{a1}K^\Theta_{a2}}{[H^+]^2 + [H^+]K^\Theta_{a1} + K^\Theta_{a1}K^\Theta_{a2}} $$

Ka1, Ka2 = 5.9e-2, 6.5e-5 # 默认数据是草酸
pH = np.arange(0,14,0.1)
dH2A, dHA, dA = [], [], []
for i in pH:
    H = 10**-i
    div = H**2 + H*Ka1 + Ka1*Ka2
    dH2A.append(H**2/div)
    dHA.append(H*Ka1/div)
    dA.append(Ka1*Ka2/div)

plt.figure(figsize=(8,5))
plt.plot(pH, dH2A, label='$H_2A$')
plt.plot(pH, dHA, label='$HA$')
plt.plot(pH, dA, label="$A^-$")
plt.xlim([0,14]), plt.ylim([0,1])
plt.xlabel('pH'), plt.ylabel('$\delta$'), plt.legend()
plt.show()