荧光寿命显微镜的原理及其相图的Python绘制(Phasor Plot for FLIM-FRET)
首先简单说明荧光寿命
- 荧光寿命是指荧光分子在被激发后,能量从激发态回落至基态所需时间的一半($t_{1/2}$),是荧光分子的固有物理性质(在没有其他因素干扰时,通常是一个常数),是荧光分子除了在波长、偏振、强度之外的另一可以用以挖掘的角度
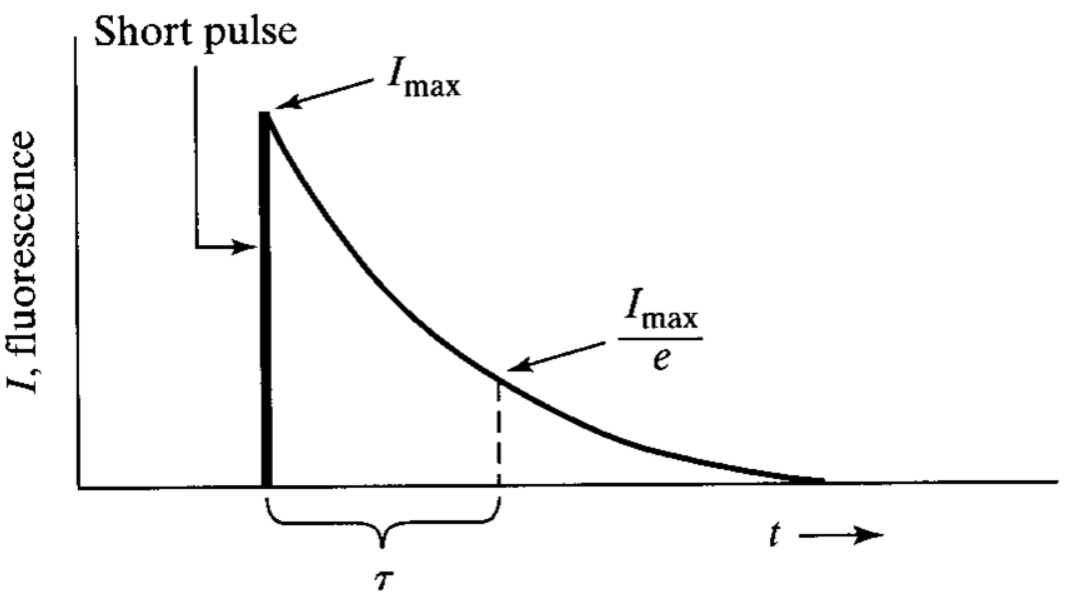
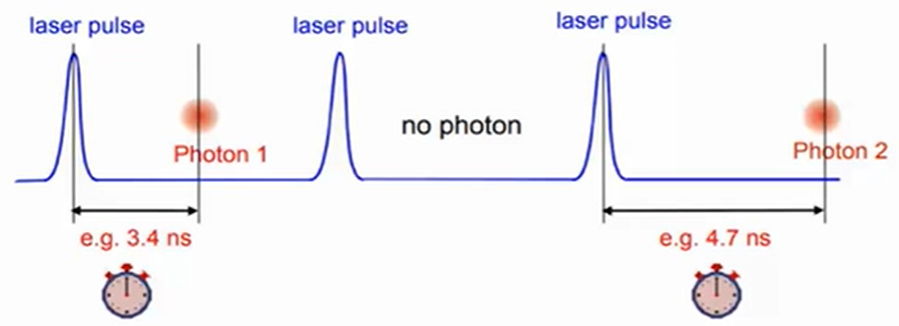
- 荧光寿命的测量需要使用荧光寿命显微镜(FLIM),目前最常用的测量方法是时间相关单光子记数法(Time-Correlated Single-Photon Counting ,TCSPC),该方法是在短时间激活荧光分子后,连续一段时间测量光强(光子个数),从而绘制出荧光强度的衰减曲线,并在此基础上拟合指数函数
-
激活的频率是需要适应测量荧光分子的寿命,因为需要等待一段时间进行测量,这个时间太长和太短都不好,生物荧光分子的寿命通常在12ns以下,因而多使用80MHz的频闪激光作为光源
-
在实际的图像采集过程中,是在每个像素格子内激活进行测量,为了得到足够的光子数进行数据拟合,通常会Frame Repetitiors 10次
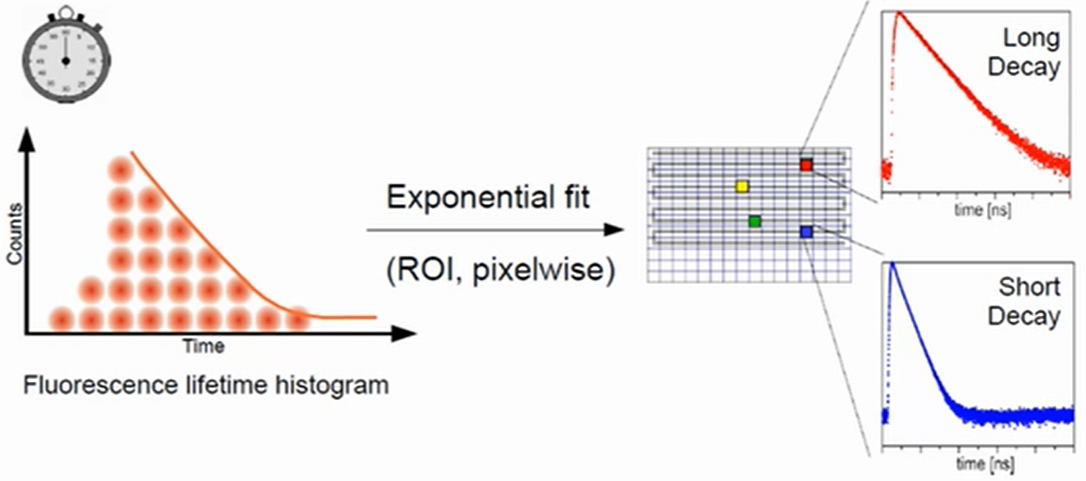
- 对数据的拟合使用指数衰减的模型,其中$\tau$为荧光寿命,$i$是为了区分不同像素位置,$n$指代10次重复,$A$是最大强度,$Bkgr$是背景强度,$IRF$是仪器响应函数 $$ y(t) = ( \sum_{i=0}^{n} A[i] e^{-\frac{t}{\tau[i]}} + Bkgr ) ※ IRF $$ 最后,数据拟合后得到的效果如下图所示,每个像素点都有一个对应的寿命值,需要划定一个信号区域(ROI)求取平均来得到最终的寿命值,该值需要通过卡方检测
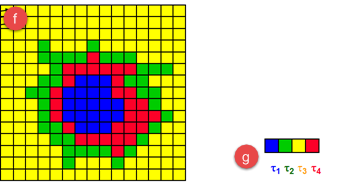
- 如果生物样品中含有多种荧光分子(混合着不同的荧光寿命),也可以修改模型为多个指数衰减,拟合多个寿命值
关于相图(Phasor Plot)
简单说,相图就是对荧光寿命的数据做傅里叶变换,拆分出频域空间的信号,然后将每一个点的频率信号值画在单位圆上。假设其衰减曲线的信号为指数函数,则可以推到出其在频域空间中横纵轴的计算公式为:
$$ g_{i,j}(\omega) = \frac {\int_0^\infty I_{i,j}(t) cos(\omega t) dt}{\int_0^\infty I_{i,j}(t)dt} $$
$$ s_{i,j}(\omega) = \frac {\int_0^\infty I_{i,j}(t) sin(\omega t) dt}{\int_0^\infty I_{i,j}(t)dt} $$
两者间也必然存在如下关系,说明标准的样品,其荧光信号应该落在这个半圆上
$$ s_{i,j}^2 + (g_{i,j} - \frac12)^2 = \frac14 $$
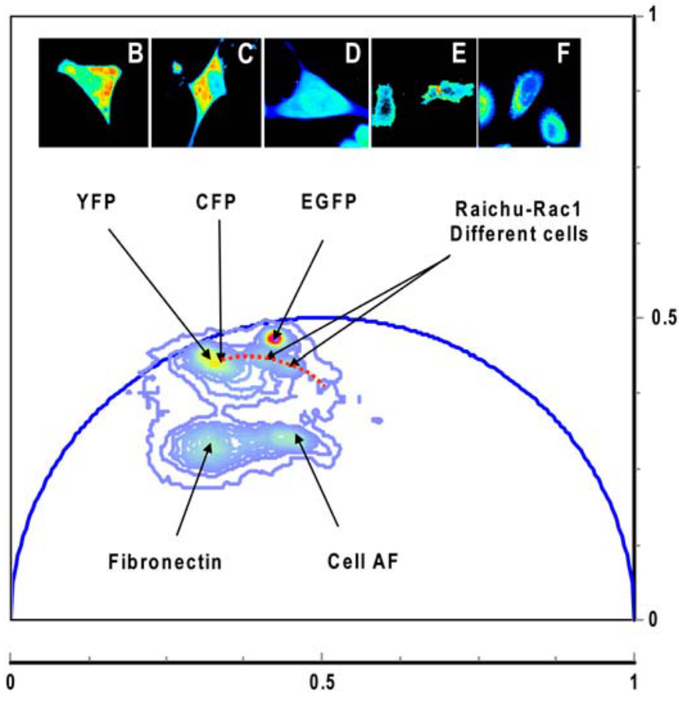
在频域空间,信号的叠加符合向量加法。因而当荧光拍摄出多个组分时,其信号可能落在单位半圆内部,此时可以将其做向量分解,找到组成其信号的可能组分。
使用Python手绘荧光寿命的Phasor Plot
因为FLIM的数据分析会占据获取有效数据的一多半时间,而显微镜配套的分析处理软件是商业化不公开的,为了节省机时,故将FLIM采集的数据导出为标准格式
.ptu,自己回来处理数据;通过指数拟合获得寿命的代码网络上已经有很多了,甚至有imageJ插件直接使用,但更为合理的Phasor分析方法却没有可行的方案,看着算法并不是很困难就自己动手了
1、引包,需要引入FLIM标准格式.ptu读取模块、计算模块numpy、绘图模块matplotlib和seaborn,PTUreader是来自于Github上pull下来的库后微调得到的(原代码也可以直接使用)
from readPTU_FLIM import PTUreader
from matplotlib import pyplot as plt
from numpy import fft
import numpy as np
import seaborn as sns
from tqdm import tqdm
sns.set(style='white', palette='muted', color_codes=True)2、读入.ptu格式文件,并展示图像;
fpath = '211015Image007.ptu'
f = PTUreader(fpath, print_header_data = False)
flim_data_stack, intensity_image = f.get_flim_data_stack()
plt.imshow(intensity_image)
plt.colorbar()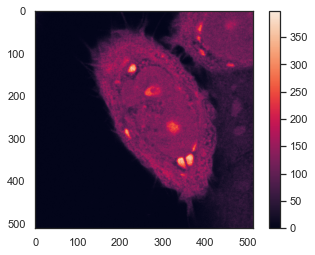
使用flim_data_stack.shape可以看到数据的结构,本次数据为(512, 512, 2, 138),即图像采集尺寸为512×512,包含两个通道(mNG和DAPI),以及在两次脉冲激活间记录了138个时间点信息(80MHz的激光脉冲理论上应该间隔12.5ns,在数据的头文件中f.head['MeasDesc_Resolution']会包含这一数值)
3、可以将所有像素的光子数加起来,观察这个指数衰减图像
plt.figure(figsize=(15,6))
x = np.sum(np.sum(flim_data_stack[:,:,0,:], axis=1), axis=0)
plt.plot(x)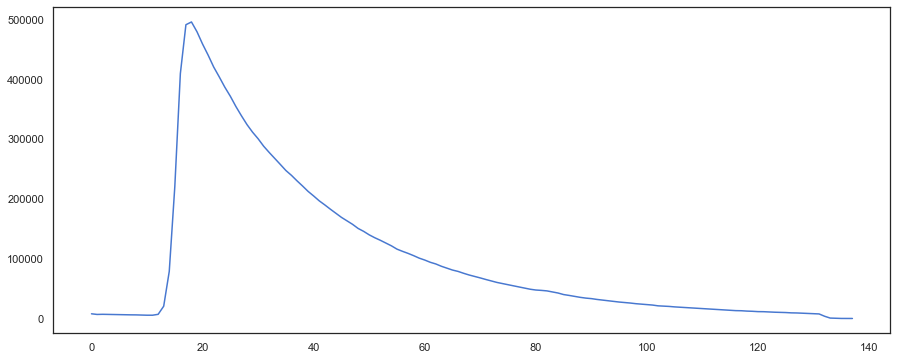
4、通过快速傅里叶变换,计算绘制Phasor图
K = flim_data_stack.shape[3]+1
T = f.head['MeasDesc_Resolution']
omega = 2*np.pi/(K*T)
semicircle = [[], []]
for i in np.arange(0, 100, 0.01):
semicircle[0].append(1/(1+(i)**2))
semicircle[1].append(i/(1+(i)**2))
result = []
for i,x in tqdm(enumerate(flim_data_stack)):
for j,y in enumerate(x):
d = y[0][20:]
dd = d/sum(d)
if sum(d)<=100:
continue
ft = np.fft.fft(dd)
result.append([ft.real[1], -ft.imag[1], intensity_image[i, j]])
step = flim_data_stack.shape[3] - 20
t = np.linspace(0,step*T, step)
ruler = []
for tau in range(1,11):
tau = tau*1e-9
y = np.exp(t/tau)
ynorm = y/sum(y)
ft = np.fft.fft(ynorm)
ruler.append([ft.real[1], ft.imag[1]])
g = [i[0] for i in result]
s = [i[1] for i in result]
gr = [i[0] for i in ruler]
sr = [i[1] for i in ruler]
plt.scatter(g, s)
plt.scatter(gr, sr, marker='o', color='r')
# plt.xlim([0,1])
# plt.ylim([0,1])
plt.gca().set_aspect(1)
plt.plot(semicircle[0], semicircle[1], color='black', linewidth=1)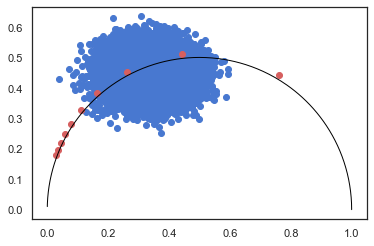
使用seaborn绘制出的、好看一点的密度图,看起来和软件输出的有点像了
result = np.array(result)
plt.figure(figsize=(10,10))
plt.xlim([0,1])
plt.ylim([0,1])
plt.gca().set_aspect(1)
plt.plot(semicircle[0], semicircle[1], color='black', linewidth=1)
sns.kdeplot(result[:,0], result[:,1], cmap='Reds', shade=True)
plt.scatter(gr, sr, marker='o', color='b')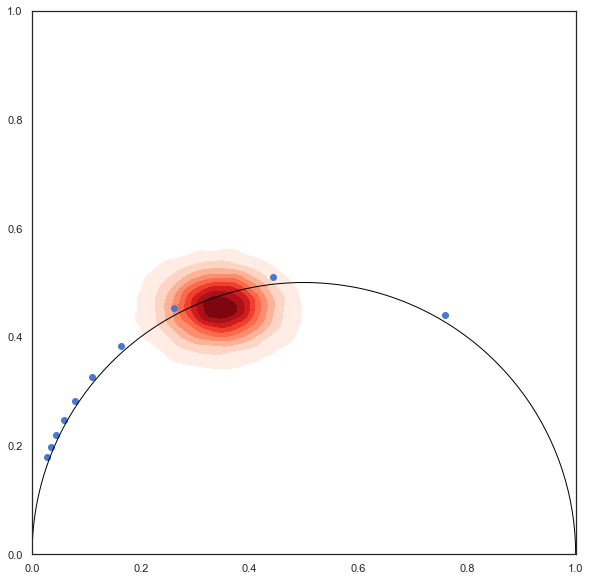
PS:关于这个图上通过FFT得到的刻度点和通过解析几何计算得到的标准半圆之间存在位移,老实说还没来得及去探究太多,初步推测是因为使用了高精度浮点数计算导致结果不准确,之后需要正式用这个图了再想办法解决
