OpenCV | 空间域处理之邻域操作/几何变换/形态学操作
在给定图像的像素上直接进行运算的方法称之为图像空间域的处理;而根据所操作的像素的多少和类型分为:
- 单像素操作(点运算):即对单个像素点进行处理
- 邻域操作:即对某一像素点的操作与该点周围的其他点相关
- 几何变换:对整张图片进行全局性的操作
- 形态学操作:对特定图像形状(边界、凸壳等)的处理或操作
本文介绍空间域处理的后面四种,其主要有如下几种常见操作:各类的卷积/滤波、几何变换(图像的平移、旋转、裁剪等)、形态学操作(腐蚀、膨胀、开运算、闭运算等)等;
八、各类的卷积/滤波
什么是卷积/滤波?可以用来做什么?
-
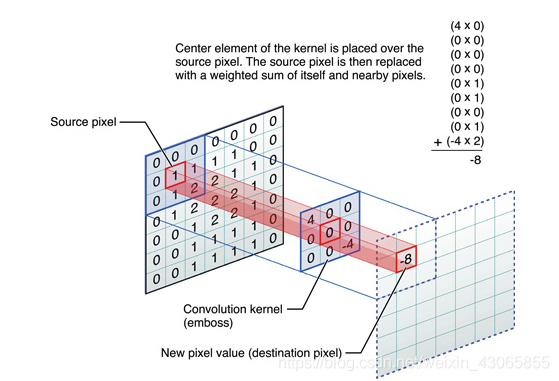
卷积是一种邻域操作,是滤波器的一种;其计算它的邻域像素和滤波器矩阵的对应元素的乘积,然后加和作为该像素位置的值,在对图像的每一个像素点做同样的处理之后,得到一幅新的图片,达到滤波的效果;
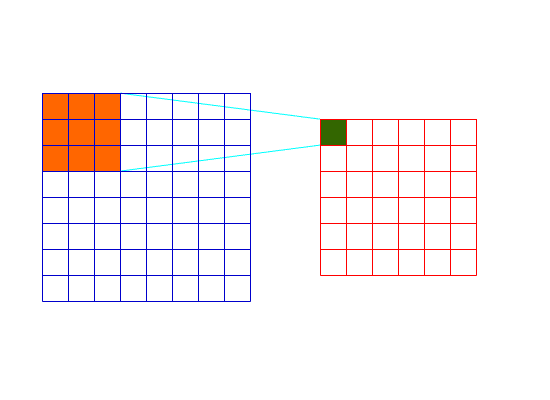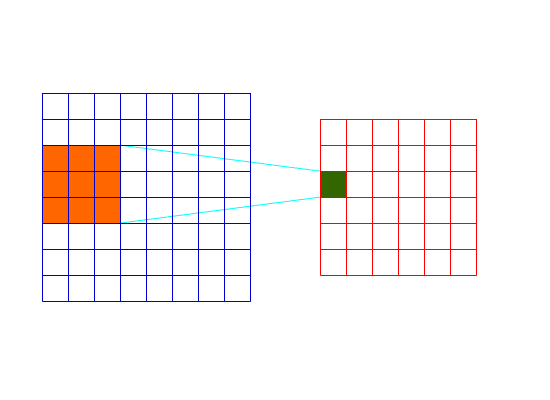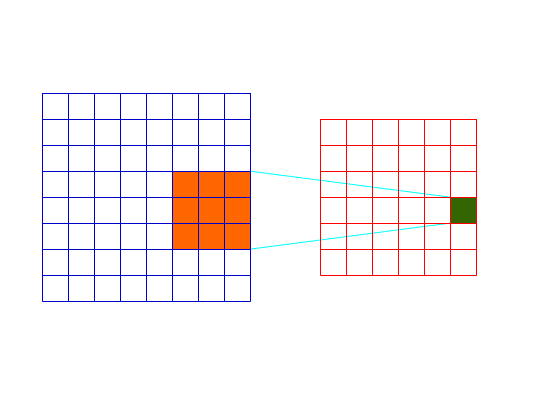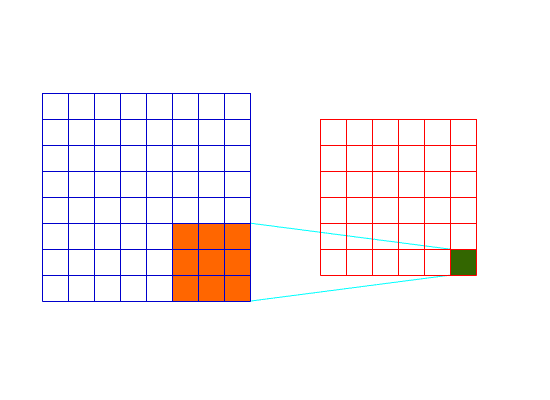
-
其具体的计算公式为:
$$ h(x,y)=\sum_{k,l}f(k,l)\cdot I(x+k,y+l) $$
其中,$f(k,l)$为滤波器,$I(x,y)$为图片上的像素点,$h(x,y)$为滤波器处理后的结果
-
滤波器具有不同的尺寸大小,其内填充的值也有很多不同的类型,不同的填充值可以带来不同的效果,如中值滤波可以去除椒盐噪声,高斯滤波可以使图像模糊、平滑,梯度Sobel滤波可以检测边缘等;
-
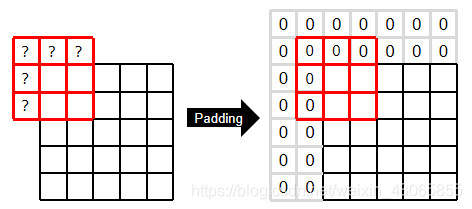
在滤波操作时往往会在边界出现收缩的情况,此时我们可以使用边界填充(Padding)的方法使得滤波后图像尺寸与原图一致;具体发填充方法有补零、边界复制、镜像、块复制等;
-
此外,卷积核每次移动的步长(step)也会影响图像最终的大小;
-
在opencv中,提供了
cv2.filter2D()这个函数供我们自定义卷积,其参数包含有:
-
src为原图片,ddepth为目标图像的深度,目前先不纠结该参数,直接填写-1表示输出图像深度保持与原图像相同 (详见Sobel算子);
-
kernel是单通道的卷积核矩阵,可以为一个Numpy数组;
-
anchor表示卷积核与图片的相对位置,默认值(-1, -1)表示卷积核正中间的位置代表在图像上扫描的位置;
-
delta为一个常数值,即求和后可以再加一个常数作为修正因子;
-
borderType即为之前所述的边缘填充方式,常见的类型有
cv2.BORDER_CONSTANT(用常数值i填充),cv2.BORDER_REPLICATE(复制边界像素),cv2.BORDER_REFLECT(反射边界像素填充)等等,更多信息可以参考
-
均值滤波
均值滤波相当于对邻域空间求平均数操作,其使用$1/N$作为所有元素的值(所有参数和为1);
在opencv中,我们有两种方法使用均值,一个是借助Numpy构建卷积核然后调用cv2.filter2D()函数,另外opencv也对常用的滤波器提供了现成的方法,cv2.boxblur(img, kernel-size)或cv2.blur(img, kernel-size)完成,kernel-size为元组表示的卷积核尺寸,其卷积核不仅仅可以为正方形,也可以为矩形,如(1, 10)(瘦高卷积核)可以实现垂直方向上的模糊、矮胖卷积核实现水平方向的模糊;
如下使用5×5卷积核的测试效果,已然可见其边界已不再清楚:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
kernel = np.ones((5,5),np.float32)/25
dst = cv2.filter2D(img,-1,kernel)
# dst = cv2.blur(img, (1, 10))
fig = plt.figure(figsize=(16,6))
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(dst[:,:,::-1]),plt.title('Averaging')
plt.xticks([]), plt.yticks([])
plt.show() 个人认为,均值滤波的应用场景不多,其有点和稀泥的感觉,既没有去除噪声点,又让图像显得不清不楚……
个人认为,均值滤波的应用场景不多,其有点和稀泥的感觉,既没有去除噪声点,又让图像显得不清不楚……
中值滤波
中值滤波是将卷积框内的像素值排序,然后取中位数作为该位置结果的一种滤波操作,其要求卷积核尺寸为奇数;
中值滤波最为人称道的应用场景在于去除含黑白细点的椒盐噪声,可以通过如下函数给图片添加上一定比例的黑白碎点模拟椒盐噪声:
import random
def sp_noise(image,prob):
output = np.zeros(image.shape,np.uint8)
thres = 1 - prob
for i in range(image.shape[0]):
for j in range(image.shape[1]):
rdn = random.random()
if rdn < prob:
output[i][j] = 0
elif rdn > thres:
output[i][j] = 255
else:
output[i][j] = image[i][j]
return output在opencv中实现中值滤波效果的函数是cv2.medianBlur(img, size),其参数传入原图和卷积核的边长即可,如下为中值滤波的测试代码和测试效果:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
img_noise = sp_noise(img, 0.01)
img_median = cv2.medianBlur(img_noise, 5)
fig = plt.figure(figsize=(18,6))
plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(img_noise[:,:,::-1]),plt.title('SP_Noise')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(img_median[:,:,::-1]),plt.title('Median')
plt.xticks([]), plt.yticks([])
plt.show()
高斯滤波
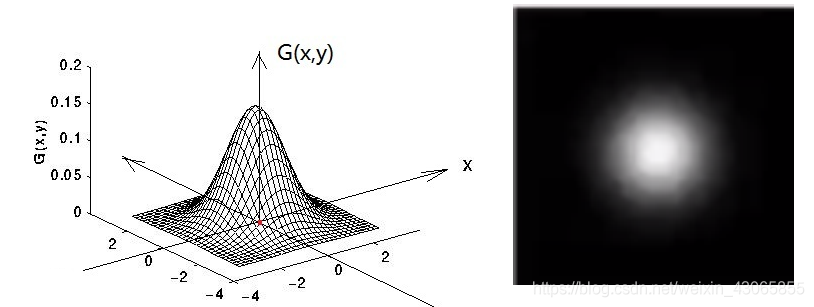
高斯分布是统计学上著名的概率分布,又称正态分布;若其扩展至二维则有二维正态分布(均值为0,$\sigma$为标准差),其表达式为:
$$
G_\sigma=\frac{1}{2\pi\sigma^2}e^-\frac{x^2+y^2}{2\sigma^2}
$$
-
高斯滤波所用的卷积核,又称为高斯核,是根据二维高斯分布计算的来的;
-
其要求卷积核为正方形,边长n为奇数,所有元素之和为1(也可以改变为其他形状或者拆解开来在两个维度上分别操作);
-
高斯分布广泛存在于自然界中,高斯噪声往往源自数字图像中的采集期间, 由于不良照明或传感器高温而引起;
-
高斯核也是模仿人眼,关注图像的中心区域,可以有效去除符合高斯分布的一些噪声,但也使得图像在一定程度上变模糊;
可以使用如下函数模拟高斯噪声:
import random
def gauss_noise(image, mean=0, var=0.001):
image = np.array(image/255, dtype=float)
noise = np.random.normal(mean, var ** 0.5, image.shape)
out = image + noise
if out.min() < 0:
low_clip = -1.
else:
low_clip = 0.
out = np.clip(out, low_clip, 1.0)
out = np.uint8(out*255)
return outopencv提供了cv2.getGaussianKernel()方法构建一个高斯核,提供了cv2.GaussianBlur()方法来实现高斯滤波,其有如下参数:

其中,src为原图像,ksize为高斯核的尺寸,以元组形式表示;sigmaX为在x方向上的标准差,sigmaY为y方向上的标准差,在sigmaX不为0时,sigmaY默认与sigmaX相等;如下为测试代码和效果图:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
img_noise = gauss_noise(img, 0.01)
img_median = cv2.GaussianBlur(img_noise, (5,5), 0.5)
fig = plt.figure(figsize=(18,6))
plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(img_noise[:,:,::-1]),plt.title('Gaussian_Noise')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(img_median[:,:,::-1]),plt.title('GaussianBlur')
plt.xticks([]), plt.yticks([])
plt.show() 在高斯模糊的作用下,有如下规律:
在高斯模糊的作用下,有如下规律:
- 在核大小固定的情况下,sigma值越大,权值分布越平缓,邻域各个点的值对输出值的影响越大,图像越模糊
- 在核大小固定的情况下,sigma值越小,权值分布越突起,邻域各个点的值对输出值的影响越小,图像受到的影响也越小
- sigma固定时,核越大图像越模糊,核越小图像受到的影响越小。
双边滤波
双边滤波是高斯滤波器的一种改进形式,其不仅仅考虑了像素之间的空间关系,也考虑像素值之间灰度值的相似性。双边滤波同时使用空间高斯权重和灰度值相似性高斯权重。空间高斯函数确保只有邻近区域的像素对中心点有影响,灰度值相似性高斯函数确保只有与中心像素灰度值相近的才会被用来做模糊运算。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
blur = cv2.bilateralFilter(img,9,75,75)
fig = plt.figure(figsize=(15,6), dpi=80)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('Blurred')
plt.xticks([]), plt.yticks([])
plt.show()
除了模糊图像,卷积的另一大作用是边缘检测;卷积虽然仅是一个矩阵,但其仍可以实现梯度的计算;首先来认识什么是梯度?
梯度,简单说是在二维连续函数的偏导数,即 $$ \frac{\partial f(x,y)}{\partial x}=\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x} \\ \frac{\partial f(x,y)}{\partial x}=\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y} $$ 而图像是一个二维的离散数集,我们可以定义其梯度为: $$ \nabla f\equiv grad(f)\equiv[g_x,g_y]^T=[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]^T \\ g_x=\frac{\partial f(x,y)}{\partial x}={f(x+\Delta x,y)-f(x,y)} \\ g_y=\frac{\partial f(x,y)}{\partial x}={f(x,y+\Delta y)-f(x,y)} $$ 梯度是对图像的偏导数进行计算和检测,当连续图像上偏导数突然变大或变小就意味着原图的像素颜色出现了剧烈变化,即可能出现了边缘;因而我们可以通过计算偏导数来实现对边缘的检测;而梯度的计算本质上仍是一种邻域操作,可以通过也卷积操作实现;下面是几个常见的梯度滤波
梯度Roberts滤波
当$\Delta x=1$时,则水平梯度为右侧格子值—当前侧格子值,垂直梯度为0;当$\Delta y=1$时,则水平梯度为0,垂直梯度为下侧格子值—当前格子值;故在两格子的卷积核中可以构建Roberts梯度为: $$ kernel_x=\begin{bmatrix} -1 & 1 \end {bmatrix}, kernel_y=\begin{bmatrix} -1 \\ 1 \end {bmatrix} $$ $kernel_x$为水平梯度,检测垂直边缘;$kernel_y$为垂直梯度,检测水平边缘;如下代码使用了基础卷积核的2倍以使检测效果增强显示;
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
kernel_x = np.array([[-2],[2]])
kernel_y = np.array([[-2,2]])
dst_x = cv2.filter2D(img,-1,kernel_x)
dst_y = cv2.filter2D(img,-1,kernel_y)
fig = plt.figure(figsize=(16,6))
plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(dst_x[:,:,::-1]),plt.title('Roberts_x')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(dst_y[:,:,::-1]),plt.title('Roberts_y')
plt.xticks([]), plt.yticks([])
plt.show()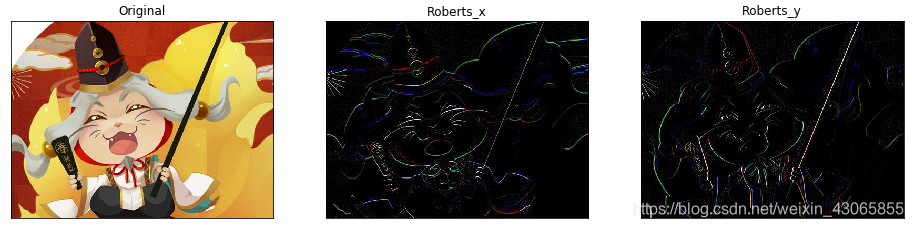
梯度Prewitt滤波
Prewitt仍可以理解为水平或垂直梯度,但是其在另一个方向上乘以了均值平滑的效果(如下图):
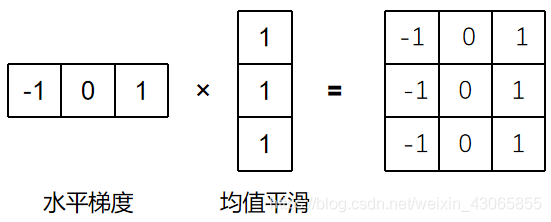
因而可以得到了类似的卷积核,甚至可以将其扩展到斜线上;其卷积核如下: $$ kernel_x=\begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end {bmatrix},\ kernel_y=\begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end {bmatrix}\ kernel_{lr}=\begin{bmatrix} 0 & 1 & 1 \\ -1 & 0 & 1 \\ -1 & -1 & 0 \end {bmatrix},\ kernel_{rl}=\begin{bmatrix} -1 & -1 & 0 \\ -1 & 0 & 1 \\ 0 & 1 & 1 \end {bmatrix} $$ 其中,$kernel_x$由水平梯度扩展而来检测垂直边缘;$kernel_y$由垂直梯度扩展而来检水平边缘;$kernel_{lr}$梯度为左下右上方向,可以检测左上右下边缘;$kernel_{rl}$梯度为左上右下方向,可以检测左下右上边缘;
如下为构建卷积核并执行Prewitt滤波操作的代码和测试结果,dst为左右滤波结果的加和:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
kernel_x = np.array([[-1,-1,-1],[0,0,0],[1,1,1]])
kernel_y = np.array([[-1,0,1],[-1,0,1],[-1,0,1]])
kernel_lr = np.array([[0,1,1],[-1,0,1],[-1,-1,0]])
kernel_rl = np.array([[-1,-1,0],[-1,0,1],[0,1,1]])
dst_x = cv2.filter2D(img,-1,kernel_x)
dst_y = cv2.filter2D(img,-1,kernel_y)
dst_lr = cv2.filter2D(img,-1,kernel_lr)
dst_rl = cv2.filter2D(img,-1,kernel_rl)
dst = dst_x+dst_y+dst_lr+dst_rl
fig = plt.figure(figsize=(16,8))
plt.subplot(231),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(232),plt.imshow(dst_x[:,:,::-1]),plt.title('Prewitt_x')
plt.xticks([]), plt.yticks([])
plt.subplot(233),plt.imshow(dst_y[:,:,::-1]),plt.title('Prewitt_y')
plt.xticks([]), plt.yticks([])
plt.subplot(234),plt.imshow(dst[:,:,::-1]),plt.title('Prewitt')
plt.xticks([]), plt.yticks([])
plt.subplot(235),plt.imshow(dst_lr[:,:,::-1]),plt.title('Prewitt_lr')
plt.xticks([]), plt.yticks([])
plt.subplot(236),plt.imshow(dst_rl[:,:,::-1]),plt.title('Prewitt_rl')
plt.xticks([]), plt.yticks([])
plt.show()
梯度Sobel滤波
Sobel算子是在Prewitt算子的基础上改进而来,其将梯度乘以高斯平滑器,从而使其能够较好的抑制(平滑)噪声,其卷积核如下: $$ kernel_x=\begin{bmatrix} -1 & 0 & 1 \end {bmatrix} \times \begin{bmatrix} 1 \ 2 \ 1 \end {bmatrix}=\begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end {bmatrix}\ $$
$$ kernel_y=\begin{bmatrix} 1 & 2 & 1 \end {bmatrix} \times \begin{bmatrix} -1 \ 0 \ 1 \end {bmatrix}=\begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end {bmatrix} $$ 如下为构建卷积核和执行Sobel滤波的代码和测试结果(原图和前面一致):
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
kernel_x = np.array([[-1,-2,-1],[0,0,0],[1,2,1]])
kernel_y = np.array([[-1,0,1],[-2,0,2],[-1,0,1]])
kx = cv2.filter2D(img,-1,kernel_x)
ky = cv2.filter2D(img,-1,kernel_y)
sobel = kx+ky
fig = plt.figure(figsize=(16,8))
plt.subplot(131),plt.imshow(sobel[:,:,::-1]),plt.title('Sobel')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(kx[:,:,::-1]),plt.title('Sobel_x')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(ky[:,:,::-1]),plt.title('Sobel_y')
plt.xticks([]), plt.yticks([])
plt.show()
此外,opencv还提供了cv2.Sobel()函数来完成边缘检测的工作,其包含如下参数:

- src为原图为原图片,ddepth为图像的深度,-1表示采用的是与原图像相同的深度(需要注意的是目标图像的深度必须大于等于原图像的深度 )
- dx,dy为在x和y方向上求导的阶数,可以为0、1、2;
- ksize为构建的Sobel算子的大小,可以为-1、1、3、5、7 ;
- 其余量与之前在卷积操作时的解释相同,这里不再赘述;
这里着重解释两个参量:
第一个为ksize,opencv保留了-1值给Scharr滤波器,其是Sobel的改进,据说在相同的运算速度下有更好的表现,如下为其卷积核的形状: $$ kernel_x=\begin{bmatrix} -3 & 0 & 3 \\ -10 & 0 & 10 \\ -3 & 0 & 3 \end {bmatrix},\ kernel_y=\begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ 3 & 10 & 3 \end {bmatrix}\ $$ 如下为测试代码和结果:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
sobel = cv2.Sobel(img, -1,1,0,ksize=3)
scharr = cv2.Sobel(img, -1, 1, 0, ksize=-1)
fig = plt.figure(figsize=(18,6))
plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(sobel[:,:,::-1]),plt.title('Sobel_x')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(scharr[:,:,::-1]),plt.title('Scharr_x')
plt.xticks([]), plt.yticks([])
plt.show()
第二个参量为ddepth,即图像深度,之前我们始终给其赋值为-1,即与原图保留一致的深度,但实际上其可以有更多的选择;opencv中对图像的深度可以有如下表示: $$ CV <bit\ depth>(S|U|F)C<number\ of\ channels> $$
- bit_depth为图像的位深度,即几个二进制位表示像素值
- S|U|F表示数据类型,S位带符号整数,U为无符号整数,F为浮点数
- 在表示图像Mat的格式时还会在后面写上Cx表示含有x个通道
一般图的深度为np.int8/CV_8U,即8位二进制数表示的整数(0-255),在当Sobel算子进行求导操作时,负数值丢失为0,这样就仅能检测由黑至白的边界,而不能检测由白至黑的边界,如下为使用一个白色box的图所作的测试效果:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/box.png',0)
sobelx8u = cv2.Sobel(img,cv2.CV_8U,1,0,ksize=5)
sobelx64f = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=5)
abs_sobel64f = np.absolute(sobelx64f)
sobel_8u = np.uint8(abs_sobel64f)
plt.subplot(1,3,1),plt.imshow(img,cmap = 'gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(1,3,2),plt.imshow(sobelx8u,cmap = 'gray')
plt.title('Sobel CV_8U'), plt.xticks([]), plt.yticks([])
plt.subplot(1,3,3),plt.imshow(sobel_8u,cmap = 'gray')
plt.title('Sobel abs(CV_64F)'), plt.xticks([]), plt.yticks([])
plt.show() 为了解决这一问题,我们需要改换图像的深度,以获得完全的信息,如可以将图像深度改为
为了解决这一问题,我们需要改换图像的深度,以获得完全的信息,如可以将图像深度改为 cv2.CV_16S或cv2.CV_64F 来保留负数的结果,最后在显示时再使用np.absolute()将其取绝对值展示,或使用cv2.convertScaleAbs()再将其转化为CV_8U展示:
如下为测试代码:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
sobel_0 = cv2.Sobel(img, -1,1,0,ksize=3)
sobel_1 = cv2.Sobel(img, cv2.CV_64F,1,0,ksize=3)
# laplacian = cv2.Laplacian(img,cv2.CV_64F)
dst = cv2.convertScaleAbs(sobel_1)
fig = plt.figure(figsize=(18,6))
plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(sobel_0[:,:,::-1]),plt.title('Sobel_x(CV_8U)')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(dst[:,:,::-1]),plt.title('Sobel_x(CV_64F)')
plt.xticks([]), plt.yticks([])
plt.show()
梯度Laplacian滤波
Laplacian滤波是一个二阶微分算子,其可以检测一个点周围明显高/低的像素值,在边缘检测中可以识别像素值快速变化的区域,其构建方程为: $$ \Delta f=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} $$
$$ 1D = \begin{bmatrix} 1 & -2 & 1 \end{bmatrix} ,\ 2D_4 = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end {bmatrix},\ 2D_8 = \begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end {bmatrix} $$ 如下为Laplacian滤波的检测代码和结果:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
kernel4 = np.array([[0,1,0],[1,-8,1],[0,1,0]])
kernel8 = np.array([[1,1,1],[1,-8,1],[1,1,1]])
Lplc4 = cv2.filter2D(img,-1,kernel4)
Lplc8 = cv2.filter2D(img,-1,kernel8)
fig = plt.figure(figsize=(18,6))
plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(Lplc4[:,:,::-1]),plt.title('Laplacian-4')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(Lplc8[:,:,::-1]),plt.title('Laplacian-8')
plt.xticks([]), plt.yticks([])
plt.show()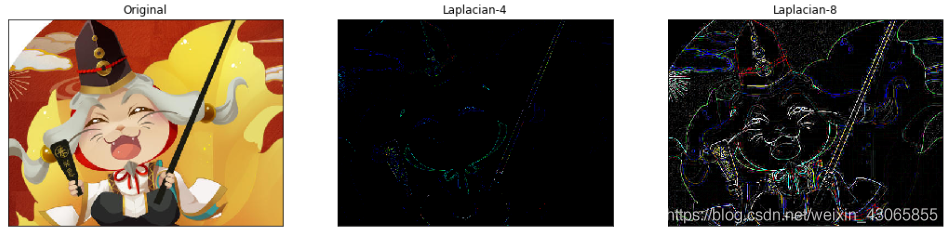
需要注意的是,opencv还提供了cv2.Laplacian()函数,其同样可以完成Laplacian滤波的工作,其具体的用法与cv2.Sobel()一致,这里不再赘述;
锐化滤波
锐化内核强调在相邻的像素值的差异,可以使图像看起来更生动;如下为测试代码和结果:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg')
kernel = np.array([[1,1,1],[1,-8,1],[1,1,1]])
Lplc = cv2.filter2D(img,-1,kernel)
fig = plt.figure(figsize=(18,6))
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(Lplc[:,:,::-1]),plt.title('Laplacian')
plt.xticks([]), plt.yticks([])
plt.show()
九、图像的几何变换
OpenCV提供了两个变换函数,cv2.warpAffine()和cv2.warpPerspective(),使用这两个函数结合不同的变换矩阵,可以实现所有类型的变换:
cv2.warpAffine()接收的参数是2 × 3 的变换矩阵cv2.warpPerspective()接收的参数是 3 × 3 的变换矩阵
其所包含的参数有:

- src为原图,M为变换矩阵,dsize为目标图像的尺寸
平移
平移就是将图片对象移换一个位置;若沿(x,y)方向移动的距离是$(t_x, t_y)$,你可以以下面的方式构建移动矩阵:
$$
\begin{bmatrix}
1 & 0 & t_x \\
0 & 1 & t_y
\end{bmatrix}
$$
你可以使用Numpy数组构建这个矩阵(数据类型是np.float32),然后把它传给函数cv2.warpAffine(),下例即将原图移动了(100,50)个像素:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/01.jpg',1)
rows,cols = img.shape[0:2]
M = np.float32([[1,0,100],[0,1,50]])
dst = cv2.warpAffine(img,M,(cols,rows))
fig = plt.figure(figsize=(18,6))
plt.subplot(121), plt.imshow(img[:,:,::-1]), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(dst[:,:,::-1]), plt.xticks([]), plt.yticks([])
plt.show()
旋转
若以$(x,y)$为旋转中心,逆时针旋转$\theta$时,其旋转矩阵构造为
$$
\begin{bmatrix}
\alpha & \beta & (1-\alpha)\cdot center x-\beta \cdot center y \\
-\beta & \alpha & \beta \cdot center x+(1-\alpha)\cdot center y
\end{bmatrix}
$$
其中:
$$
\alpha = scale \cdot \cos\theta,\ \beta = scale \cdot \sin\theta
$$
为了简便地构建这个旋转矩阵,OpenCV提供了cv2.getRotationMatrix2D()函数,该函数包含3个参数:
- 旋转中心$(x,y)$
- 逆时针旋转角度 θ
- 缩放因子,小于1时缩小,大于1时放大
下面的例子是在不缩放的情况下,以(0, rows)点(左下角)为中心,将图像逆时针旋转30度:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img=cv2.imread('image/01.jpg',1)
rows,cols=img.shape[0:2]
M=cv2.getRotationMatrix2D((0, rows),30,0.8)
dst=cv2.warpAffine(img,M,(cols,rows))
fig = plt.figure(figsize=(18,6))
plt.subplot(121), plt.imshow(img[:,:,::-1])
plt.subplot(122), plt.imshow(dst[:,:,::-1])
plt.show()
仿射变换
三点确定一个平面,当给出原图像中的三个点以及他们在输出图像中的位置,可以将原图进行仿射变换;在仿射变换后,原图中所有的平行线在结果图像中同样平行;可以将变换前后的点集传入cv2.getAffineTransform函数,创建一个2x3的变换矩阵,后将这个矩阵会被传给函数 cv2.warpAffine()得到变换结果;
具体看下面的例子(蓝色的点为选择的点坐标):
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/grid.png')
rows,cols,ch = img.shape
pts1 = np.float32([[20,20],[20,80],[80,20]])
pts2 = np.float32([[20,30],[20,90],[80,20]])
M = cv2.getAffineTransform(pts1,pts2)
dst = cv2.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()
透视变换
在给出4个不共线的点时,我们可以对齐作透视变换,指定其变换前后的位置传入cv2.getPerspectiveTransform()函数可以构建一个3×3的变换矩阵,将其传入cv2.warpPerspective()函数可以得到变换后的结果;具体的测试代码和效果图如下:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/grid2.png')
rows,cols,ch = img.shape
pts1 = np.float32([[20,10],[10,80],[90,80],[80,10]])
pts2 = np.float32([[0,0],[0,100],[100,100],[100,0]])
M = cv2.getPerspectiveTransform(pts1,pts2)
dst = cv2.warpPerspective(img,M,(rows,cols))
fig = plt.figure(figsize=(8,4), dpi=80)
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()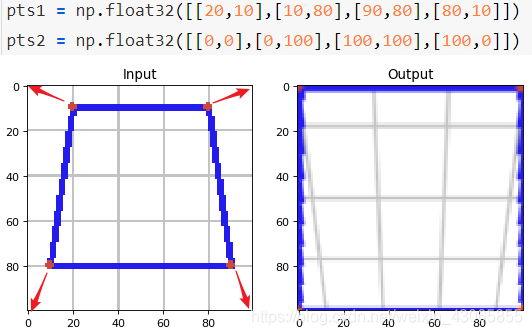
缩放扩展
扩展缩放只是改变图像的尺寸大小而不改变其内容,OpenCV提供的函cv2.resize()可以实现这个功能;图像的尺寸可以自己手动设置,也可以指定缩放因子fx,fy;
此外,interpolation参数可以指定使用不同的插值方法 ,其具体方法总结如下表:
| FLAG | 对应算法 |
|---|---|
| INTER_NEAREST | 最临近插值算法 |
| INTER_LINEAR | 线性插值算法 |
| INTER_CUBIC | 双立方插值算法 |
| INTER_AREA | 区域插值算法(使用像素区域关系的重采样,时图像抽取的首选方法,但是当图像被放大,它类似于INTER_NEAREST方法) |
| INTER_LANCZOS4 | Lanczos插值(超过8x8邻域的插值算法) |
| INTER_MAX | 用于插值的掩模板 |
| WARP_FILL_OUTLIERS | 标志位,用于填充目标图像的像素值,如果其中的一些值对应于原图像中的异常值,那么这些值将被设置为0 |
| WARP_INVERSE_MAP | 标志位,反变换 |
默认情况下所有改变图像尺寸大小的操作使用的插值方法都是cv2.INTER_LINEAR,官方文档 在缩放时我们推荐使用cv2.INTER_AREA,在扩展时我们推荐使用cv2.INTER_CUBIC(慢) 和 cv2.INTER_LINEAR; |
import cv2
import numpy as np
from matplotlib import pyplot as plt
img=cv2.imread('image/01.jpg')
res=cv2.resize(img,None,fx=2,fy=2,interpolation=cv2.INTER_CUBIC)
# height,width=img.shape[:2]
# res=cv2.resize(img,(2*width,2*height),interpolation=cv2.INTER_CUBIC)
fig = plt.figure(figsize=(12,5), dpi=80)
plt.subplot(121), plt.imshow(img[:,:,::-1])
plt.subplot(122), plt.imshow(res[:,:,::-1])
plt.show()
十、形态学处理
腐蚀
如果定义如下操作:“当卷积核沿着图像滑动,如果与卷积核对应的原图像的所有像素值都不为0,那么中心元素就保持原来的像素值,否则就变为零”,经过这样的操作,我们可以得到图像边缘向内收缩的结果,就像被腐蚀一样;腐蚀操作可以有效地去除白噪点,也可以将细线相连的两部分形状断开;
opencv提供cv2.erdoe()函数来执行该操作:

- src为原图,kernel为卷积核,除了Numpy构建数组外,这里介绍另一种构建卷积核的方法
cv2.getStructuringElement(MORPH, size),其中第一个参数为形状,第二个参数描述卷积核的大小; - 形状参数可以为
cv2.MORPH_ELLIPSE(椭圆)、cv2.MORPH_RECT(矩形)、cv2.MORPH_CROSS(十字)等;卷积核大小为元组形式;
如下为测试代码和效果图:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/test.png',0)
kernel = np.ones((3,3),np.uint8)
erosion = cv2.erode(img,kernel,iterations = 1)
fig = plt.figure(figsize=(12,6), dpi=80)
plt.subplot(121),plt.imshow(img, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(erosion, cmap='gray'),plt.title('Close')
plt.xticks([]), plt.yticks([])
plt.show()
从效果图可见,其不仅减小了噪声点的大小,也断开了字体中的细线连接;
膨胀
与腐蚀相反,膨胀操作为:“与卷积核对应的原图像的像素值中只要有一个是 1,中心元素的像素值就是 1”,所以这个操作会扩展图像中的白色区域(前景);opencv中有cv2.dilate()方法来完成膨胀操作,其用法与腐蚀相同;如下为测试代码和效果图:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/test.png',0)
kernel = np.ones((3,3),np.uint8)
dilation = cv2.dilate(img,kernel,iterations = 1)
fig = plt.figure(figsize=(12,6), dpi=80)
plt.subplot(121),plt.imshow(img, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(dilation, cmap='gray'),plt.title('Close')
plt.xticks([]), plt.yticks([])
plt.show()
开运算 / 闭运算
先腐蚀再膨胀的操作称为开运算,其往往被用于去除噪声,因为腐蚀在去掉白噪声的同时,也会使前景对象变小,对其进行膨胀操作可使前景恢复而不影响噪声;
先膨胀再腐蚀的操作叫做闭运算,其可以填充白色前景中的黑色小洞;
opencv中使用cv2.morphologyEx()函数传入cv2.MORPH_OPEN或cv2.MORPH_CLOSE参数时进行开运算/闭运算操作;如下为测试代码和效果图:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img_c = cv2.imread('image/test.png',0)
kernel = np.ones((4,4),np.uint8)
opening = cv2.morphologyEx(img, cv2.MORPH_OPEN, kernel)
closing = cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel)
fig = plt.figure(figsize=(12,6), dpi=80)
plt.subplot(131),plt.imshow(img_c, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(closing, cmap='gray'),plt.title('Close')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(opening, cmap='gray'),plt.title('Open')
plt.xticks([]), plt.yticks([])
plt.show()
礼帽 / 黑帽
礼帽(又称顶帽),是原图与开运算之间的差值;opencv中使用cv2.morphologyEx()函数传入cv2.MORPH_TOPHAT参数时进行礼帽操作;如下为测试代码和效果图:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/test.png',0)
kernel = np.ones((4,4),np.uint8)
opening = cv2.morphologyEx(img, cv2.MORPH_OPEN, kernel)
tophat = cv2.morphologyEx(img, cv2.MORPH_TOPHAT, kernel)
fig = plt.figure(figsize=(16,10), dpi=80)
plt.subplot(131),plt.imshow(img_c, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(opening, cmap='gray'),plt.title('Open')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(tophat, cmap='gray'),plt.title('Tophat')
plt.xticks([]), plt.yticks([])
plt.show()
黑帽是原图与闭运算之间差值;opencv中使用cv2.morphologyEx()函数传入cv2.MORPH_BLACKHAT参数时进行礼帽操作;如下为测试代码和效果图:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img_c = cv2.imread('image/test.png',0)
kernel = np.ones((4,4),np.uint8)
closing = cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel)
blackhat = cv2.morphologyEx(img, cv2.MORPH_BLACKHAT, kernel)
fig = plt.figure(figsize=(16,10), dpi=80)
plt.subplot(131),plt.imshow(img_c, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(closing, cmap='gray'),plt.title('Close')
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(blackhat, cmap='gray'),plt.title('Blackhat')
plt.xticks([]), plt.yticks([])
plt.show()
形态学梯度
opencv中使用cv2.morphologyEx()函数传入cv2.MORPH_GRADIENT参数时求解形态学的梯度,其被定义为膨胀后图像减去腐蚀后图像所得到的边框;
此外,也有内部梯度(原图减腐蚀)和外部梯度(膨胀减原图)的说法,其可以通过cv2.substract(img1, img2)实现;如下为测试结果:
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('image/test.png',0)
kernel = np.ones((4,4),np.uint8)
gradient = cv2.morphologyEx(img, cv2.MORPH_GRADIENT, kernel)
erosion = cv2.erode(img,kernel,iterations = 1)
dilation = cv2.dilate(img,kernel,iterations = 1)
inner = cv2.subtract(img, erosion)
outer = cv2.subtract(dilation, img)
fig = plt.figure(figsize=(12,6), dpi=80)
plt.subplot(221),plt.imshow(img, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(222),plt.imshow(gradient, cmap='gray'),plt.title('Gradient')
plt.xticks([]), plt.yticks([])
plt.subplot(223),plt.imshow(inner, cmap='gray'),plt.title('Inner_gradient')
plt.xticks([]), plt.yticks([])
plt.subplot(224),plt.imshow(outer, cmap='gray'),plt.title('Outer_gradient')
plt.xticks([]), plt.yticks([])
plt.show() 2020年4月7日 本性之初
2020年4月7日 本性之初
